Teorema Menelaus merupakan dual dari teorema Ceva.
Jika kalian melihat pembuktian dari teorema Ceva yang sebelumnya, sebenarnya pembuktian teorema ini memiliki proses yang sama.
Untuk Kondisi Pertama:
Di kondisi ini, kita menemui 2 kasus YANG MEMUNGKINKAN:
*******************************************************************************************
Kasus 1: jika ada 1 titik yang berada di perpanjangan garis, 2 titik lainnya ada di garis yang bukan merupakan perpanjangan. Artinya, garis ini melewati daerah segitiga ABC. Lihat gambar.

Kasus 2: Jika semua titik berada pada perpanjangan garis. Artinya, garis tidak melewati daerah segitiga ABC. Lihat gambar.
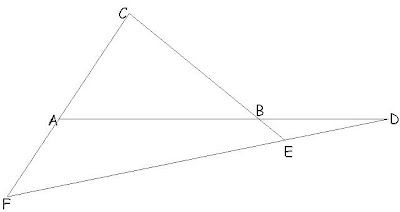
Dengan menggunakan prinsip kesebangunan segitiga, maka kita akan mendapatkan persamaan berikut.
 ... (i)
... (i)
 ... (ii)
... (ii)
 ... (iii)
Dengan mengalikan ketiganya, lagi-lagi teorema Menelaus TERBUKTI.
... (iii)
Dengan mengalikan ketiganya, lagi-lagi teorema Menelaus TERBUKTI.
*******************************************************************************************
Untuk Kondisi Kedua:
Sekarang, kita ingin membuktikan kalau titik D,E, dan F' segaris jika terpenuhi kondisi berikut:
 Dengan masih mengganggap titik F ada dalam segitiga di mana titik D, E, dan F segaris (sesuai dengan pembuktian kondisi 1), maka persamaan ini juga berlaku:
Dengan masih mengganggap titik F ada dalam segitiga di mana titik D, E, dan F segaris (sesuai dengan pembuktian kondisi 1), maka persamaan ini juga berlaku:
 Dengan menggabungkan kedua persamaan itu kita dapatkan:
Dengan menggabungkan kedua persamaan itu kita dapatkan:
 Tambahkan 1 di kedua ruas (cara yang sama seperti pembuktian teorema Ceva), maka:
Tambahkan 1 di kedua ruas (cara yang sama seperti pembuktian teorema Ceva), maka:



 Artinya, titik
Artinya, titik  dan titik
dan titik berhimpit. Jadi, titik D,E, dan F' segaris. TERBUKTI.
berhimpit. Jadi, titik D,E, dan F' segaris. TERBUKTI.
=========================================================================
Sekian post mengenai pembuktian Teorema Menelaus yang sedikit membosankan.. Padahal, teorema ini sangat menarik untuk bisa dibuktikan.. ^^
Jika ada di antara kalian yang masih bingung membaca post pembuktian ini, silakan tanya saja di comment. Aku akan bersedia menjawab..
Btw, mengertikah kalian dengan tulisan post ini? Tell me... ^^
Diberikan sebuah segitiga ABC. Titik D, E, dan F masing-masing terletak pada garis (atau perpanjangan garis) dari AB, BC, dan CA.
Teorema Menelaus menyatakan bahwa:
Titik D, E, dan F segaris jika dan hanya jika:

Tanda negatif disebabkan karena adanya ruas garis yang memiliki arah berlawanan (panjang yang negatif). Logikanya, AD+DB=AB.. Dengan demikian, salah satu dari AD atau DB haruslah negatif.
Teorema Menelaus menyatakan bahwa:
Titik D, E, dan F segaris jika dan hanya jika:

Tanda negatif disebabkan karena adanya ruas garis yang memiliki arah berlawanan (panjang yang negatif). Logikanya, AD+DB=AB.. Dengan demikian, salah satu dari AD atau DB haruslah negatif.
Tantangan: Dengan melihat proses seperti pembuktian teorema Ceva, kalian tentunya bisa menyelesaikan pembuktian teorema ini dengan mudah. Jadi, buktikanlah sendiri tanpa melihat post ini.
=========================================================================
BUKTI TEOREMA MENELAUS
Jika kalian melihat pembuktian dari teorema Ceva yang sebelumnya, sebenarnya pembuktian teorema ini memiliki proses yang sama.
Perhatikan kata "jika dan hanya jika" dari teorema tersebut.
Dengan demikian, untuk membuktikan teorema ini, kita harus membuktikan 2 kondisi berikut:
1. Jika titik D, E, dan F segaris, maka
2. Jika , maka titik D, E, dan F segaris.
, maka titik D, E, dan F segaris.
Dengan demikian, untuk membuktikan teorema ini, kita harus membuktikan 2 kondisi berikut:
1. Jika titik D, E, dan F segaris, maka

2. Jika
 , maka titik D, E, dan F segaris.
, maka titik D, E, dan F segaris.Untuk Kondisi Pertama:
Di kondisi ini, kita menemui 2 kasus YANG MEMUNGKINKAN:
*******************************************************************************************
Kasus 1: jika ada 1 titik yang berada di perpanjangan garis, 2 titik lainnya ada di garis yang bukan merupakan perpanjangan. Artinya, garis ini melewati daerah segitiga ABC. Lihat gambar.

Sekarang, kita buktikan dahulu untuk kasus 1:
Proyeksikan setiap titik-titik sudut segitiga ke garis DEF.
Dengan menggunakan prinsip kesebangunan segitiga, kita dapatkan 3 persamaan berikut:
 ... (i)
... (i)
 ...(ii)
...(ii)
 ...(iii)
Dengan mengalikan ketiganya, maka akan kita dapatkan teorema Menelaus:
...(iii)
Dengan mengalikan ketiganya, maka akan kita dapatkan teorema Menelaus:

TERBUKTI
*******************************************************************************************
Proyeksikan setiap titik-titik sudut segitiga ke garis DEF.
Dengan menggunakan prinsip kesebangunan segitiga, kita dapatkan 3 persamaan berikut:
 ... (i)
... (i) ...(ii)
...(ii) ...(iii)
...(iii)
TERBUKTI

Sekarang, kita akan membuktikan kasus 2 dengan cara yang sama seperti kasus 1:
Proyeksikan setiap titik-titik sudut segitiga ke garis DEF.
Proyeksikan setiap titik-titik sudut segitiga ke garis DEF.
 ... (i)
... (i) ... (ii)
... (ii) ... (iii)
... (iii)*******************************************************************************************
Untuk Kondisi Kedua:
Sekarang, kita ingin membuktikan kalau titik D,E, dan F' segaris jika terpenuhi kondisi berikut:







 dan titik
dan titik berhimpit. Jadi, titik D,E, dan F' segaris. TERBUKTI.
berhimpit. Jadi, titik D,E, dan F' segaris. TERBUKTI.=========================================================================
Sekian post mengenai pembuktian Teorema Menelaus yang sedikit membosankan.. Padahal, teorema ini sangat menarik untuk bisa dibuktikan.. ^^
Jika ada di antara kalian yang masih bingung membaca post pembuktian ini, silakan tanya saja di comment. Aku akan bersedia menjawab..
Btw, mengertikah kalian dengan tulisan post ini? Tell me... ^^
Sumber:http://planetmath.org/?op=getobj&from=objects&id=3092, dan http://en.wikipedia.org/wiki/Menelaus_theorem



0 Komentar