Bukti: Deret Taylor
Konsep deret ini sungguh tidak sulit jika kita sudah mengenal konsep derivatif. Sangat Mudah..
Berikut adalah formula yang dikenal dengan nama Deret Taylor.
Formula yang menakjubkan, bukan? Mungkin beberapa dari kalian sudah sakit mata, melihat formula -- yang sepertinya jatuh dari langit. Di post ini, akan dijelaskan segala konsepnya mulai dari dari dasar (namun, tetap saja kalian harus paham konsep turunan, key? ^^).
=========================================================================
(**bagian ini dapat di-skip demi kenyamanan mata**)
Sebelum beranjak ke pembuktian Deret Taylor, alangkah baiknya kita ketahui dulu adanya Teorema Taylor. Teorema ini diperkenalkan oleh orang yang sama, yaitu Brook Taylor (1715), yang bunyi teoremanya sbb.
Di sini, dibuktikan secara konsep.
Kita tak akan menemukan kesulitan membuktikan teorema itu jika
merupakan polinomial.
Untuk yang polinomial, diberikan sebuah contoh sbb.
Contoh Soal:
Diketahui
. Dengan 
, berapakah nilai dari 
, 
, 
, 
, dst, yang memenuhi persamaan berikut?
Jawab:
Fungsi di atas merupakan polinomial yang berderajat 3. Oleh karena itu, kita tidak perlu memperhatikan derajat yang lebih besar dari 3, seperti
, dan seterusnya. Artinya, nilai yang perlu dicari adalah nilai , , , dan saja. (sisanya bernilai nol).
Soal ini dapat dikerjakan dengan penjabaran biasa (yang sesungguhnya, akan lebih efektif menggunakan formula deret taylor).
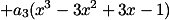
Setelah dikalikan dan dijumlahkan menjadi sbb:
Dengan menghubung-hubungkan koefisien ruas kiri dan kanan, kita akan menemukan jawabannya:
, 
, 
, dan 
. Jawaban ini tentunya unik.
Bisa kita lihat alasannya dari pengerjaan di atas. Nilai, , , dan didapatkan secara paralel dalam koefisien-koefisien dari x.
Bagaimana dengan fungsi yang bukan polinomial?
Fungsi yang bukan polinomial, seperti
, 
, dan sebagainya dapat kita hampiri sebagai fungsi polinomial berderajat tak hingga. Masalah pun beres!!. Teorema pun terbukti untuk semua fungsi.. ^^
=========================================================================
Dari Teorema Taylor, didapat fungsi yang didefinisikan sbb:
Bagaimana jika fungsi tersebut kita turunkan 1 kali, 2 kali dan seterusnya? Hasilnya ditunjukkan di bawah.
...
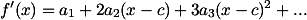
... (dst)
Kemudian, pada fungsi awal dan fungsi-fungsi turunan tersebut, jika kita menetapkan
, maka:
...
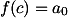
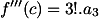
... (dst)
Dengan memasukkan harga, , , , dst, maka Deret Taylor pun terbukti.
(Note: Di sini, terdapat syarat implisit yang mengharuskan
terdefinisi. Ini merupakan pelengkap dari syarat Taylor seperti yang sudah dijelaskan di atas. ^^)
=========================================================================
Deret Taylor banyak memiliki kegunaan. Intinya, deret taylor mampu menghampiri suatu fungsi secara polinomial.. Masih bingung? Kenapa kita tidak melihat salah satu kegunaan deret Taylor yang terbesar dan paling mendasar di post INI. ^^
Ada yang ingin ditanyakan?? :D
Berikut adalah formula yang dikenal dengan nama Deret Taylor.
Untuk setiap fungsi yang diferensiabel di titik c, maka berlaku ekspansi dari sebagai berikut.
yang diferensiabel di titik c, maka berlaku ekspansi dari sebagai berikut.Formula yang menakjubkan, bukan? Mungkin beberapa dari kalian sudah sakit mata, melihat formula -- yang sepertinya jatuh dari langit. Di post ini, akan dijelaskan segala konsepnya mulai dari dari dasar (namun, tetap saja kalian harus paham konsep turunan, key? ^^).
=========================================================================
Teorema Taylor
(**bagian ini dapat di-skip demi kenyamanan mata**)
Untuk fungsi yang diferensiabel di titik c, maka hanya akan terdapat 1 fungsi yang memenuhi kondisi berikut.
yang diferensiabel di titik c, maka hanya akan terdapat 1 fungsi yang memenuhi kondisi berikut.Di sini, dibuktikan secara konsep.
Kita tak akan menemukan kesulitan membuktikan teorema itu jika
merupakan polinomial.Untuk yang polinomial, diberikan sebuah contoh sbb.
Contoh Soal:
Diketahui
. Dengan , berapakah nilai dari , , , , dst, yang memenuhi persamaan berikut?Fungsi di atas merupakan polinomial yang berderajat 3. Oleh karena itu, kita tidak perlu memperhatikan derajat yang lebih besar dari 3, seperti
, dan seterusnya. Artinya, nilai yang perlu dicari adalah nilai , , , dan saja. (sisanya bernilai nol).Soal ini dapat dikerjakan dengan penjabaran biasa (yang sesungguhnya, akan lebih efektif menggunakan formula deret taylor).
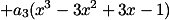
Setelah dikalikan dan dijumlahkan menjadi sbb:
Dengan menghubung-hubungkan koefisien ruas kiri dan kanan, kita akan menemukan jawabannya:
, , , dan . Jawaban ini tentunya unik.Bisa kita lihat alasannya dari pengerjaan di atas. Nilai
, , , dan didapatkan secara paralel dalam koefisien-koefisien dari x.Bagaimana dengan fungsi yang bukan polinomial?
Fungsi yang bukan polinomial, seperti
, , dan sebagainya dapat kita hampiri sebagai fungsi polinomial berderajat tak hingga. Masalah pun beres!!. Teorema pun terbukti untuk semua fungsi.. ^^=========================================================================
Bukti Deret Taylor
Dari Teorema Taylor, didapat fungsi yang didefinisikan sbb:
Bagaimana jika fungsi tersebut kita turunkan 1 kali, 2 kali dan seterusnya? Hasilnya ditunjukkan di bawah.
...
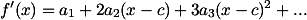
... (dst)
Kemudian, pada fungsi awal dan fungsi-fungsi turunan tersebut, jika kita menetapkan
, maka:...
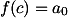
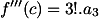
... (dst)
Dengan memasukkan harga
, , , , dst, maka Deret Taylor pun terbukti.(Note: Di sini, terdapat syarat implisit yang mengharuskan
terdefinisi. Ini merupakan pelengkap dari syarat Taylor seperti yang sudah dijelaskan di atas. ^^)=========================================================================
Kegunaan Deret Taylor
Deret Taylor banyak memiliki kegunaan. Intinya, deret taylor mampu menghampiri suatu fungsi secara polinomial.. Masih bingung? Kenapa kita tidak melihat salah satu kegunaan deret Taylor yang terbesar dan paling mendasar di post INI. ^^
Ada yang ingin ditanyakan?? :D
Sumber: http://mathworld.wolfram.com/TaylorSeries.html, http://www.efunda.com/math/taylor_series/taylor_series.cfm, http://en.wikipedia.org/wiki/Taylor_series, dan buku Kalkulus I (Wikaria Gazali).