Pembuktian Teorema Ceva LENGKAP
Teorema Ceva merupakan teorema yang terkenal di geometri elementer.
=========================================================================
Untuk Kondisi Pertama:
Diketahui bahwa garis AD, BE, dan CF berpotongan di 1 titik.
Lihat gambar segitiga ABC di atas.
 dan
dan  memiliki tinggi yang sama.
memiliki tinggi yang sama.
Oleh karena itu: ... (ia)
... (ia)
Perhatikan juga bahwa dan
dan  juga memiliki tinggi yang sama.
juga memiliki tinggi yang sama.
Oleh karena itu: ...(ib)
...(ib)
Dari kedua persamaan di atas, maka kita dapatkan:

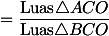 ... (ic)
... (ic)
Dengan cara yang sama, kita akan mendapatkan persamaan untuk sisi segitiga yang lain:
 ... (ii)
... (ii)
 ... (iii)
... (iii)
Kalikan ketiga persamaan itu, maka akan kita dapatkan:

(Gunakan gambar segitiga di atas, dengan simbol dan garis yang sama)
Terdapat titik F' pada garis AB sehingga memenuhi persamaan berikut.
 ... (i)
Karena kita masih memakai simbol F dalam gambar kita, maka persamaan ini juga berlaku (sesuai dengan pembuktian yang kondisi pertama):
... (i)
Karena kita masih memakai simbol F dalam gambar kita, maka persamaan ini juga berlaku (sesuai dengan pembuktian yang kondisi pertama):
 ... (ii)
... (ii)
Persamaan terakhir menunjukkan bahwa titik  dan titik
dan titik berhimpit.
berhimpit.
Artinya garis garis AD, BE, dan CF' berpotongan di 1 titik
Lihat juga post mengenai PEMBUKTIAN DALIL SINUS di SINI.
Untuk segitiga ABC, dalil Sinus berbunyi sbb: .
.
Maka, kita dapatkan ketiga persamaan berikut (lihat gambar paling atas).
 ... (i)
... (i)
 ... (ii)
... (ii)
 ... (iii)
Dengan mengalikan ketiga persamaan tersebut, kita dapatkan persamaan berikut.
... (iii)
Dengan mengalikan ketiga persamaan tersebut, kita dapatkan persamaan berikut.

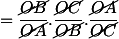

=========================================================================
Sekian dulu post tentang pembuktian ini. Teorema ini sering dipakai untuk kasus-kasus geometri segitiga yang sederhana. Untuk contoh soal, akan diberikan di post lain, bukan di sini.. ^^
Lihat juga mengenai Teorema Menelaus (the dual of Ceva Theorem). ^^
Diberikan sebuah segitiga ABC dengan titik D, E, dan F masing-masing terletak pada garis BC, CA, dan AB. (lihat gambar)
Teorema Ceva menyatakan bahwa

Sesuai dengan dalil Sinus, Teorema Ceva juga dapat dibentuk sebagai berikut.

Teorema Ceva menyatakan bahwa
Garis AD, BE, dan CF berpotongan di 1 titik jika dan hanya jika:

Sesuai dengan dalil Sinus, Teorema Ceva juga dapat dibentuk sebagai berikut.

=========================================================================
BUKTI TEOREMA CEVA
Perhatikan kata "jika dan hanya jika" dari teorema tersebut.
Dengan demikian, untuk membuktikan teorema ini, kita harus membuktikan 2 kondisi berikut:
1. Jika garis AD, BE, dan CF berpotongan di 1 titik, maka
2. Jika , maka garis AD, BE, dan CF berpotongan di 1 titik
, maka garis AD, BE, dan CF berpotongan di 1 titik
Dengan demikian, untuk membuktikan teorema ini, kita harus membuktikan 2 kondisi berikut:
1. Jika garis AD, BE, dan CF berpotongan di 1 titik, maka

2. Jika
 , maka garis AD, BE, dan CF berpotongan di 1 titik
, maka garis AD, BE, dan CF berpotongan di 1 titikUntuk Kondisi Pertama:
Diketahui bahwa garis AD, BE, dan CF berpotongan di 1 titik.
Lihat gambar segitiga ABC di atas.
 dan
dan  memiliki tinggi yang sama.
memiliki tinggi yang sama.Oleh karena itu:
 ... (ia)
... (ia)Perhatikan juga bahwa
 dan
dan  juga memiliki tinggi yang sama.
juga memiliki tinggi yang sama.Oleh karena itu:
 ...(ib)
...(ib)Dari kedua persamaan di atas, maka kita dapatkan:

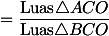 ... (ic)
... (ic)Dengan cara yang sama, kita akan mendapatkan persamaan untuk sisi segitiga yang lain:
 ... (ii)
... (ii) ... (iii)
... (iii)Kalikan ketiga persamaan itu, maka akan kita dapatkan:

Kondisi pertama TERBUKTI
Untuk Kondisi Kedua:(Gunakan gambar segitiga di atas, dengan simbol dan garis yang sama)
Terdapat titik F' pada garis AB sehingga memenuhi persamaan berikut.
 ... (i)
... (i) ... (ii)
... (ii)
Dengan membandingkan keduanya, maka kita dapatkan:
 Tambahkan 1 di kedua ruas, maka:
Tambahkan 1 di kedua ruas, maka:









 dan titik
dan titik berhimpit.
berhimpit.Artinya garis garis AD, BE, dan CF' berpotongan di 1 titik
Kondisi Kedua TERBUKTI
=========================================================================
BENTUK TEOREMA CEVA DALAM TRIGONOMETRI
Lihat juga post mengenai PEMBUKTIAN DALIL SINUS di SINI.
Untuk segitiga ABC, dalil Sinus berbunyi sbb:
 .
. ... (i)
... (i) ... (ii)
... (ii) ... (iii)
... (iii)
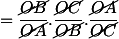

TERBUKTI.
Sekian dulu post tentang pembuktian ini. Teorema ini sering dipakai untuk kasus-kasus geometri segitiga yang sederhana. Untuk contoh soal, akan diberikan di post lain, bukan di sini.. ^^
Lihat juga mengenai Teorema Menelaus (the dual of Ceva Theorem). ^^







 , maka:
, maka:




 habis dibagi 200. Tentukan bilangan bulat
habis dibagi 200. Tentukan bilangan bulat  yang mungkin.
yang mungkin. bersisa 1 jika dibagi 1331. Tentukan bilangan bulat
bersisa 1 jika dibagi 1331. Tentukan bilangan bulat  koin.
koin.  bersisa 67 jika dibagi 3500. Tentukanlah jumlah koin minimum yang dimiliki Budi.
bersisa 67 jika dibagi 3500. Tentukanlah jumlah koin minimum yang dimiliki Budi.
 bersisa 4 jika dibagi 15. Tentukan bilangan bulat
bersisa 4 jika dibagi 15. Tentukan bilangan bulat 



 .
.


 adalah fungsi polinomial dengan koefisien integer.
adalah fungsi polinomial dengan koefisien integer. adalah bilangan prima.
adalah bilangan prima.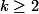 dan
dan  integer
integer adalah solusi dari
adalah solusi dari 
 , maka akan ada solusi unik integer
, maka akan ada solusi unik integer  dimana
dimana  yang memenuhi
yang memenuhi  .
.
 adalah invers dari
adalah invers dari modulo
modulo  DAN
DAN 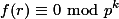 ,maka
,maka untuk semua integer
untuk semua integer ,maka
,maka
 habis dibagi 97. Tentukan bilangan bulat
habis dibagi 97. Tentukan bilangan bulat 
 , lalu periksa satu semi satu apakah
, lalu periksa satu semi satu apakah  habis dibagi 97. Namun, cara ini sungguh membuat frustasi...
habis dibagi 97. Namun, cara ini sungguh membuat frustasi...
 . Karena 97 adalah bilangan prima, maka
. Karena 97 adalah bilangan prima, maka  .
.


 .
. . Karena 1 memenuhi dan yang lainnya tidak, maka solusinya adalah
. Karena 1 memenuhi dan yang lainnya tidak, maka solusinya adalah  .
.
 dimana
dimana  . Jadi, kita dapat menerapkan sifat (i) pada (ii).
. Jadi, kita dapat menerapkan sifat (i) pada (ii).



 dan
dan  selalu habis dibagi 25. Oleh karenanya dapat kita tiadakan.
selalu habis dibagi 25. Oleh karenanya dapat kita tiadakan.
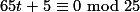
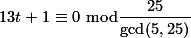







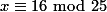
 .
. adalah
adalah  .
. .
. karena
karena  yang berarti 2 adalah invers dari 3 modulo 5.
yang berarti 2 adalah invers dari 3 modulo 5.

 .
.
 , maka kongruensi di atas dapat dipecah menjadi 2, yaitu:
, maka kongruensi di atas dapat dipecah menjadi 2, yaitu: ... (i)
... (i) . Kita dapatkan
. Kita dapatkan
 ...(i)
...(i) ... (ii)
... (ii)





 .
.

 .
.




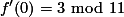 .
. , karena 4 adalah invers dari 3 modulo 11. Atau bisa ditulis
, karena 4 adalah invers dari 3 modulo 11. Atau bisa ditulis 


 .
. , karena 1 adalah invers dari 1 modulo 11. Atau bisa ditulis
, karena 1 adalah invers dari 1 modulo 11. Atau bisa ditulis  .
.
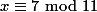

 , karena 6 adalah invers dari 2 modulo 11. Atau bisa ditulis 2x6 = 1 mod 11.
, karena 6 adalah invers dari 2 modulo 11. Atau bisa ditulis 2x6 = 1 mod 11.
 .
.



 .
.

 .
.














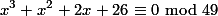


 , karena 2 adalah invers dari 4 modulo 7 Atau bisa ditulis 2x4 = 1 mod 7.
, karena 2 adalah invers dari 4 modulo 7 Atau bisa ditulis 2x4 = 1 mod 7.


 .
.



 .
. .
. .
.











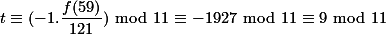
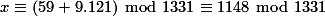 .
.

 , maka kita bisa mereduksi masalah di atas menjadi 3 bagian, yaitu:
, maka kita bisa mereduksi masalah di atas menjadi 3 bagian, yaitu: ... (i)
... (i) ... (ii)
... (ii) ... (iii)
... (iii) , maka kita dapatkan solusi sbb:
, maka kita dapatkan solusi sbb: ... (a)
... (a) .
. .
. .
.


















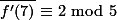












 ... (b)
... (b) ... (c)
... (c) ATAU
ATAU  ATAU
ATAU 


