Pembuktian Teorema Ptolemy Lengkap Jelas
Pembuktian Teorema Ptolemy Lengkap Jelas - Hi sobat math, matematika mungkin tak akan lepas dari kehidupan entah itu saat berinteraksi, tanpa di sadari pasti akan ada hubungan dengan matematika, oke langsung saja sesuia judul kali ini akan membahasa pembuktian teorema ptolemy, berikut penjelasannya.
Post ini membahas lagi mengenai bangun lingkaran, salah satu topik dalam geometri elementer, namun bukan lagi membahas segitiga. Teorema Ptolemy ini sangat umum, digunakan untuk mencari panjang segiempat tali busur atupun diagonal dari segiempat tali busur. Pasti dikenal di salah satu buku textbook matematika smp (namun jarang disebutkan kalau namanya Ptolemy). Dan, di textbook sangat jarang disertakan pembuktiannya. Di post ini, aku akan memberikan:
1. Bukti Teorema Ptolemy
2. Kesalahan dalam menafsirkan teorema Ptolemy (hampir 90% guru SMP salah menafsirkan teorema ini sehingga soal yang dibuat menjadi salah.)..
3. Bukti-bukti lain untuk mencari teorema ini, dan teorema yang lebih primer dari Ptolemy (dengan mencari panjang diagonal)
Post ini membahas lagi mengenai bangun lingkaran, salah satu topik dalam geometri elementer, namun bukan lagi membahas segitiga. Teorema Ptolemy ini sangat umum, digunakan untuk mencari panjang segiempat tali busur atupun diagonal dari segiempat tali busur. Pasti dikenal di salah satu buku textbook matematika smp (namun jarang disebutkan kalau namanya Ptolemy). Dan, di textbook sangat jarang disertakan pembuktiannya. Di post ini, aku akan memberikan:
1. Bukti Teorema Ptolemy
2. Kesalahan dalam menafsirkan teorema Ptolemy (hampir 90% guru SMP salah menafsirkan teorema ini sehingga soal yang dibuat menjadi salah.)..
3. Bukti-bukti lain untuk mencari teorema ini, dan teorema yang lebih primer dari Ptolemy (dengan mencari panjang diagonal)
Beginilah bunyi teorema Ptolemy:
Diberikan sebuah segiempat tali busur (atau disebut quadrilateral) ABCD yang berurutan.
Diberikan sebuah segiempat tali busur (atau disebut quadrilateral) ABCD yang berurutan.
Teorema Ptolemy menyatakan bahwa jumlah dari hasil kali sisi-sisi yang berseberangan sama dengan hasil kali diagonalnya, atau dapat ditulis sbb:
AB x CD + AD x BC = AC x BD
atau dapat ditulis begini:
ac+bd = mn
Simple sekali. Rumus ini mudah diingat. Namun, ada beberapa hal yang sebaiknya perlu kalian perhatikan. Teorema Ptolemy bisa menyesatkan jika penggunanya tidak tahu cara menggunakannya... Lihat lanjutan post di bawah.
=========================================================================
BAGIAN I
BUKTI TEOREMA PTOLEMY I
Bagaimana membuktikan teorema Ptolemy?? Dari hasil pengamatanku di internet, bukti yang paling mudah dipahami adalah bukti mengenai kesebangunan.BUKTI TEOREMA PTOLEMY I
Dari qudrilateral (gambar di atas), buatlah titik K yang terletak di diagonal DB sedemikian sehingga sudut yang dibentuk DAC sama dengan sudut BAK. Lebih jelasnya, lihat gambar di bawah.
Perhatikan bahwa
 (alasannya:
(alasannya:  dan
dan  ). Dengan demikian, kita dapatkan persamaan
). Dengan demikian, kita dapatkan persamaan  . Jika kali silang, persamaan tersebut menjadi: AC x BK = AB x CD... (i)
. Jika kali silang, persamaan tersebut menjadi: AC x BK = AB x CD... (i)Lalu, perhatikan bahwa
 (alasannya:
(alasannya:  dan
dan  ).
).Dengan demikian kita dapatkan persamaan
 . Jika dikali silang, persamaan tersebut menjadi: AC x DK = AD x BC...(ii)
. Jika dikali silang, persamaan tersebut menjadi: AC x DK = AD x BC...(ii)Selanjutnya, tinggal menambahkan kedua persamaan di atas:
AC x BK +AC x DK = AB x CD + AD x BC
AC x (BK +DK) = AB x CD + AD x BC
AC x BD = AB x CD + AD x BC
Teorema Ptolemy pun TERBUKTI.AC x (BK +DK) = AB x CD + AD x BC
AC x BD = AB x CD + AD x BC
=========================================================================
BAGIAN II
KESALAHAN-KESALAHAN DALAM QUADRILATERAL
Berikut akan diberikan beberapa contoh soal yang salah:KESALAHAN-KESALAHAN DALAM QUADRILATERAL
CONTOH SOAL SALAH I:
Diketahui segiempat talibusur ABCD dengan panjang AB = 1 cm, BC = 2 cm, CD = 3 cm, dan DA = 6 cm. Tentukan hasil kali diagonal-diagonalnya!
PENJELASAN:
Banyak orang matematika menjawab kalau hasil kali diagonalnya dapat dicari dengan teorema Ptolemy: AC x BD = AB x CD + AD x BC = 1 x 3 + 6 x 2 = 15 cm. Padahal soalnya salah.
Sampai kepala botak pun, kita tidak dapat membentuk segiempat dengan sisi masing-masing 1, 2, 3, dan 6 cm. Dengan demikian, teorema Ptolemy tidak berlaku.
CONTOH SOAL SALAH II:
Diketahui quadrilateral ABCD dengan AB = 2 cm, BC = 3 cm, CD = 4 cm, DA = 5 cm. Panjang diagonal AC = 5 cm. Tentukan panjang diagonal BD!
PENJELASAN:
Banyak orang menjawab soal itu dengan langsung memasukkannya ke teorema Ptolemy, tanpa mengecek terlebih dahulu kebenarannya. Mereka menjawabnya sbb:
BD = (AB x CD + AD + BC) / AC = (2x4+5x3)/ 5 = 4,6 cm.
Padahal, BELUM TENTU panjang diagonal AC = 5 cm. Kenyataannya panjang AC dapat dicari dengan mengetahui keempat sisinya. Begitu pula dengan panjang BD. Dengan demikian, soal tersebut salah karena yang diketahui BERLEBIH. Seharusnya, panjang diagonal AC tidak perlu diberitahukan, kecuali jika si pembuat soal benar-benar yakin jika panjang diagonal AC tersebut adalah 5 cm, dan hal ini dapat dilihat melalui perhitungan yang lain (lihat lanjutan post ini, untuk membahas hal ini)..
=========================================================================
BAGIAN III
BUKTI PRIMER TEOREMA PTOLEMY
Kita akan kembali membuktikan teorema Ptolemy, tapi dengan terlebih dahulu mencari panjang diagonal AC dan BD, kemudian keduanya dikalikan.BUKTI PRIMER TEOREMA PTOLEMY
Perhatikan kembali gambar quadrilateral berikut:
Dengan melihat
 dan menerapkan dalil Cosinus (seperti yang sudah dibahas di SINI), maka kita dapatkan persamaan:
dan menerapkan dalil Cosinus (seperti yang sudah dibahas di SINI), maka kita dapatkan persamaan:  ... (i)
... (i)Kemudian, dengan melihat
 dan menerapkan dalil cosinus lagi, maka kita dapatkan persamaan:
dan menerapkan dalil cosinus lagi, maka kita dapatkan persamaan:  . Namun, kita tahu kalau
. Namun, kita tahu kalau  (sifat quadrilateral), maka persamaan tersebut dapat ditulis ulang sbb:
(sifat quadrilateral), maka persamaan tersebut dapat ditulis ulang sbb:
 ... (ii)
... (ii)Kalikan pers (i) dengan
 , sehingga menjadi:
, sehingga menjadi: ... (ib)
... (ib) sehingga menjadi:
sehingga menjadi: ... (iib)
... (iib)




Dengan cara yang sama, kita dapatkan formula untuk menentukan panjang diagonal n.




TERBUKTI
Note: Akan lebih mudah menurunkan m dan n ketimbang menghapal rumusnya... Jadi, rumus di atas disarankan tidak dihapal demi kenyamanan otak... ^^
=========================================================================
Berikut diberikan contoh soal yang sederhana...
CONTOH SOAL:
Diketahui quadrilateral ABCD dengan AB = 2 cm, BC = 3 cm, CD = 4 cm, DA = 5 cm. Tentukan panjang diagonal AC dan BD!
JAWAB:
a = AB = 2cm.
b = BC = 3cm.
c = CD = 4cm.
d = DA = 5cm.
AC =
 =
= 
________________________=

________________________=4,411523372cm.
Panjang BD dapat ditentukan dengan 2 cara: Ptolemy atau langsung.
Cara Ptolemy:
BD =
 =
=  =
=  = 5,213618531cm.
= 5,213618531cm.Cara langsung:
BD =
 =
= 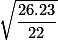 = 5,213618531cm.
= 5,213618531cm.=========================================================================
Demikian Pembuktian Teorema Ptolemy Lengkap Jelas post singkat ini dibuat.. Bukan dimaksudkan untuk membuat pusink pembaca lowh..
Masih ada lagi pembahasan mengenai quadrilateral, yaitu mencari area dan mencari jari-jari lingkarannya. Dengan itu tunggu postingan selanjutnya. Semangat para Math.
Masih ada lagi pembahasan mengenai quadrilateral, yaitu mencari area dan mencari jari-jari lingkarannya. Dengan itu tunggu postingan selanjutnya. Semangat para Math.
Sumber:http://en.wikipedia.org/wiki/Ptolemy%27s_theorem, http://www.cut-the-knot.org/proofs/ptolemy.shtml, http://www.vias.org/comp_geometry/geom_quad_cyclic.html, http://www.cut-the-knot.org/proofs/ptolemy.shtml#Mahavira


 positif integer dan
positif integer dan  adalah integer dimana
adalah integer dimana  , maka:
, maka:
 ), maka FLT berlaku:
), maka FLT berlaku:

 adalah kumpulan
adalah kumpulan  bilangan integer yang totatif (koprima) dengan
bilangan integer yang totatif (koprima) dengan  . Jadi, jumlah bilangannya harus 6.
. Jadi, jumlah bilangannya harus 6. 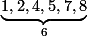 .
. 4 (mod 9)
4 (mod 9)
 adalah sistem residu yang tereduksi modulo
adalah sistem residu yang tereduksi modulo  adalah integer positif dimana
adalah integer positif dimana  , maka:
, maka: juga merupakan sistem residu yang tereduksi modulo
juga merupakan sistem residu yang tereduksi modulo  koprima dengan
koprima dengan  , maka
, maka  .
. dan
dan  yang kongruen modulo
yang kongruen modulo 

 dan
dan  inkongruen (karena keduanya berasal dari sistem
inkongruen (karena keduanya berasal dari sistem

 , maka
, maka


 .
.

 dibagi
dibagi 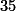 .
.





 .
.
 adalah invers dari
adalah invers dari  modulo
modulo 




 koprima dengan
koprima dengan 










 koprima, buktikan bahwa:
koprima, buktikan bahwa:
 , maka
, maka 
 , maka
, maka 





